Sorting Algorithms

Sorting is a process of ordering or placing a list of elements from a collection in some kind of order. It is nothing but storage of data in sorted order. Sorting can be done in ascending and descending order. It arranges the data in a sequence which makes searching easier.

Bubble Sort

• Bubble sort is a sorting algorithm that compares two adjacent elements and swaps them until they are not in the intended order.
• Just like the movement of air bubbles in the water that rise up to the surface, each element of the array move to the end in each iteration. Therefore, it is called a bubble sort.
• Working of Bubble Sort
• First Iteration (Compare and Swap)

• Starting from the first index, compare the first and the second elements.
• If the first element is greater than the second element, they are swapped.
• Now, compare the second and the third elements. Swap them if they are not in order.
• The above process goes on until the last element.

• Remaining Iteration
• The same process goes on for the remaining iterations.
• After each iteration, the largest element among the unsorted elements is placed at the end.

• In each iteration, the comparison takes place up to the last unsorted element.

• The array is sorted when all the unsorted elements are placed at their correct positions.

• Bubble Sort Algorithm

Selection Sort Algorithm

• Selection sort is a sorting algorithm that selects the smallest element from an unsorted list in each iteration and places that element at the beginning of the unsorted list.
• Working of Selection Sort
• Set the first element as a minimum.

• Compare minimum with the second element. If the second element is smaller than the minimum, assign the second element as a minimum.
• Compare minimum with the third element. Again, if the third element is smaller, then assign minimum to the third element otherwise do nothing. The process goes on until the last element.

• After each iteration, the minimum is placed in the front of the unsorted list.

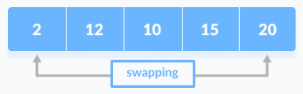
• For each iteration, indexing starts from the first unsorted element. Steps 1 to 3 are repeated until all the elements are placed at their correct positions.

• Selection Sort Algorithm

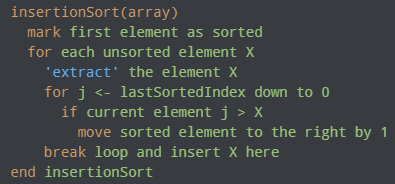
Insertion Sort Algorithm

• Insertion sort is a sorting algorithm that places an unsorted element at its suitable place in each iteration.
• Insertion sort works similarly as we sort cards in our hands in a card game.
• We assume that the first card is already sorted then, we select an unsorted card. If the unsorted card is greater than the card in hand, it is placed on the right otherwise, to the left. In the same way, other unsorted cards are taken and put in their right place.
• Working of Insertion Sort

• The first element in the array is assumed to be sorted. Take the second element and store it separately in key.
• Compare the key with the first element. If the first element is greater than the key, then the key is placed in front of the first element.

• Now, the first two elements are sorted.
• Take the third element and compare it with the elements on the left of it. Placed it just behind the element smaller than it. If there is no element smaller than it, then place it at the beginning of the array.

• Similarly, place every unsorted element at its correct position.

• Insertion Sort Algorithm

Merge Sort Algorithm

• Merge Sort is one of the most popular sorting algorithms that is based on the principle of the Divide and Conquer Algorithms.
• Here, a problem is divided into multiple sub-problems. Each sub-problem is solved individually. Finally, sub-problems are combined to form the final solution.

• Working of Merge Sort

• To understand merge sort, we take an unsorted array like the following −

• We know that merge sort first divides the whole array iteratively into equal halves unless the atomic values are achieved. We see here that an array of 8 items is divided into two arrays of size 4.

• This does not change the sequence of appearance of items in the original. Now we divide these two arrays into halves.

• We further divide these arrays and we achieve atomic value which can no more be divided.

• Now, we combine them in exactly the same manner as they were broken down. Please note the color codes given to these lists.
• We first compare the element for each list and then combine them into another list in a sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10 and in the target list of 2 values, we put 10 first, followed by 27. We change the order of 19 and 35 whereas 42 and 44 are placed sequentially.

• In the next iteration of the combining phase, we compare lists of two data values and merge them into a list of found data values placing them all in sorted order.

• After the final merging, the list should look like this −

• Merge Sort Algorithm

Quicksort Algorithm

• Quicksort is a sorting algorithm based on the divide and conquer approach where 

1. An array is divided into subarrays by selecting a pivot element (element selected from the array). While dividing the array, the pivot element should be positioned in such a way that elements less than the pivot are kept on the left side, and elements greater than the pivot are on the right side of the pivot.
2. The left and right subarrays are also divided using the same approach. This process continues until each subarray contains a single element.
3. At this point, elements are already sorted. Finally, elements are combined to form a sorted array.

• Working of Quicksort Algorithm
• Select the Pivot Element: - There are different variations of quicksort where the pivot element is selected from different positions. Here, we will be selecting the rightmost element of the array as the pivot element.

• Rearrange the Array: - Now the elements of the array are rearranged so that elements that are smaller than the pivot are put on the left and the elements greater than the pivot are put on the right. 

• Here's how we rearrange the array:
• A pointer is fixed at the pivot element. The pivot element is compared with the elements beginning from the first index.

• If the element is greater than the pivot element, a second pointer is set for that element.

• Now, the pivot is compared with other elements. If an element smaller than the pivot element is reached, the smaller element is swapped with the greater element found earlier.

• Again, the process is repeated to set the next greater element as the second pointer. And, swap it with another smaller element.

• The process goes on until the second last element is reached.

• Finally, the pivot element is swapped with the second pointer.

• Divide Subarrays: - Pivot elements are again chosen for the left and the right sub-parts separately. And, step 2 is repeated.
• The subarrays are divided until each subarray is formed of a single element. At this point, the array is already sorted.

• Quick Sort Algorithm

1. Choose the highest index value as a pivot.
2. Take two variables to point left and right of the list excluding pivot.
3. Left points to the low index.
4. Right points to the high index.
5. While value at left < (Less than) pivot move right.
6. While value at right > (Greater than) pivot move left.
7. If both Step 5 and Step 6 do not match, swap left and right.
8. If left = (Less than or Equal to) right, the point where they met is the new pivot.

Counting Sort Algorithm

• Counting sort is a sorting algorithm that sorts the elements of an array by counting the number of occurrences of each unique element in the array. The count is stored in an auxiliary array and the sorting is done by mapping the count as an index of the auxiliary array.

• Working of Counting Sort

• Find out the maximum element (let it be max) from the given array

• Initialize an array of length max+1 with all elements 0. This array is used for storing the count of the elements in the array

• Store the count of each element at their respective index in the count array
• For example: if the count of element 3 is 2 then, 2 is stored in the 3rd position of the count array. If element "5" is not present in the array, then 0 is stored in the 5th position.

• Store cumulative sum of the elements of the count array. It helps in placing the elements into the correct index of the sorted array.

• Find the index of each element of the original array in the count array. This gives the cumulative count. Place the element at the index calculated as shown in the figure below.

• After placing each element at its correct position, decrease its count by one.

• Counting Sort Algorithm

1. Iterate through the input array to find the highest value.
2. Declare a new array with the value 0 and a size of max+1.
3. Count each element in the array and increment its value in the auxiliary array generated at the corresponding index.
4. Add current and previous frequency to the auxiliary array to find the cumulative sum.
5. The cumulative value now represents the element's actual position in the sorted input array.
6. Begin iterating through the auxiliary array from 0 to max.
7. Put 0 at the corresponding index and reduce the count by 1, which will indicate the element's second position in the input array if it exists.
8. Now put the array you got in the previous step into the actual input array.

Bucket Sort Algorithm

• Bucket Sort is a sorting algorithm that divides the unsorted array elements into several groups called buckets. Each bucket is then sorted by using any of the suitable sorting algorithms or recursively applying the same bucket algorithm. Finally, the sorted buckets are combined to form a final sorted array.
• Scatter Gather Approach: - The process of bucket sort can be understood as a scatter-gather approach. Here, elements are first scattered into buckets then the elements in each bucket are sorted. Finally, the elements are gathered in order.

• Working of Bucket Sort
• Suppose, the input array is

• Create an array of size 10. Each slot of this array is used as a bucket for storing elements.

• Insert elements into the buckets from the array. The elements are inserted according to the range of the bucket.
• In our example code, we have buckets each of ranges from 0 to 1, 1 to 2, 2 to 3,...... (n-1) to n.
• Suppose, an input element is .23 is taken. It is multiplied by size = 10 (ie. .23*10=2.3). Then, it is converted into an integer (ie. 2.3≈2). Finally, .23 is inserted into bucket-2.

• Similarly, .25 is also inserted into the same bucket. Every time, the floor value of the floating-point number is taken.
• If we take integer numbers as input, we have to divide it by the interval (10 here) to get the floor value.
• Similarly, other elements are inserted into their respective buckets.

• The elements of each bucket are sorted using any of the stable sorting algorithms. Here, we have used quicksort (inbuilt function).

• The elements from each bucket are gathered.
• It is done by iterating through the bucket and inserting an individual element into the original array in each cycle. The element from the bucket is erased once it is copied into the original array.

• Bucket Sort Algorithm

1. bucket _Sort_Algorithm ()
2. Make B buckets, each of which can store a range of values for all of the buckets.
3. Fill each bucket with 0 values for all buckets.
4. Put elements in buckets that match the range for all buckets.
5. Sort elements in each bucket and gather elements from each bucket
6. end bucket_Sort_Algorithm()

Heap Sort Algorithm

• Heap Sort is a popular and efficient sorting algorithm in computer programming. Learning how to write the heap sort algorithm requires knowledge of two types of data structures - arrays and trees.
• The initial set of numbers that we want to sort is stored in an array e.g. [10, 3, 76, 34, 23, 32] and after sorting, we get a sorted array [3,10,23,32,34,76].
• Heap sort works by visualizing the elements of the array as a special kind of complete binary tree called a heap.

• Working of Heapsort Algorithm

• Heap Sort Algorithm

1. Construct a Binary Tree with the given list of Elements.
2. Transform the Binary Tree into Min Heap.
3. Delete the root element from Min Heap using the Heapify method.
4. Put the deleted element into the Sorted list.
5. Repeat the same until Min Heap becomes empty.
6. Display the sorted list.