Advanced Data Structures

Tree Data Structure

• The tree is a non-linear data structure that organizes data in a hierarchical structure and this is a recursive definition.
• If in a graph, there is one and only one path between every pair of vertices, then the graph is called a tree.
• Properties-
• There is one and only one path between every pair of vertices in a tree.
• A tree with n vertices has exactly (n-1) edges.
• A graph is a tree if and only if it is minimally connected.
• Any connected graph with n vertices and (n-1) edges is a tree.

Tree Terminology-

• Root
• The first node from where the tree originates is called a root node.
• In any tree, there must be only one root node.
• We can never have multiple root nodes in a tree data structure.
• Example

• Edge
• The connecting link between any two nodes is called an edge.
• In a tree with n number of nodes, there is exactly (n-1) number of edges.
• Example-

• Parent
• The node which has a branch from it to any other node is called a parent node.
• In other words, the node which has one or more children is called a parent node.
• In a tree, a parent node can have any number of child nodes.
• Example-

• Here,
• Node A is the parent of nodes B and C
• Node B is the parent of nodes D, E, and F
• Node C is the parent of nodes G and H
• Node E is the parent of nodes I and J
• Node G is the parent of node K
• Child
• The node which is a descendant of some node is called a child node.
• All the nodes except the root node are child nodes.
• Example-

• Here,
• Nodes B and C are the children of node A
• Nodes D, E and F are the children of node B
• Nodes G and H are the children of node C
• Nodes I and J are the children of node E
• Node K is the child of node G
• Siblings-
• Nodes that belong to the same parent are called siblings.
• In other words, nodes with the same parent are sibling nodes.
• Example-

• Here,
• Nodes B and C are siblings
• Nodes D, E, and F are siblings
• Nodes G and H are siblings
• Nodes I and J are siblings
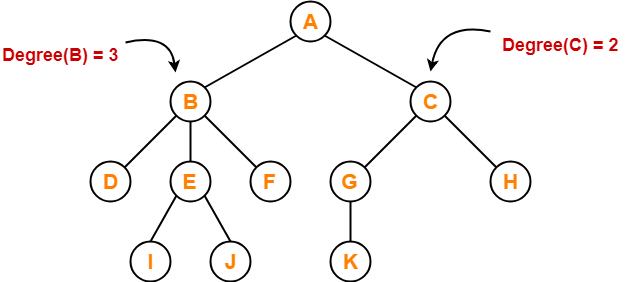
• Degree-
• The degree of a node is the total number of children of that node.
• Degree of a tree is the highest degree of a node among all the nodes in the tree.
• Example-

• Here,
• Degree of node A = 2
• Degree of node B = 3
• Degree of node C = 2
• Degree of node D = 0
• Degree of node E = 2
• Degree of node F = 0
• Degree of node G = 1
• Degree of node H = 0
• Degree of node I = 0
• Degree of node J = 0
• Degree of node K = 0
• Internal Node-
• The node which has at least one child is called as an internal node.
• Internal nodes are also called non-terminal nodes.
• Every non-leaf node is an internal node.
• Example- Here, nodes A, B, C, E, and G are internal nodes.

• Leaf Node-
• The node which does not have any child is called a leaf node.
• Leaf nodes are also called external nodes or terminal nodes.
• Example- Here, nodes D, I, J, F, K, and H are leaf nodes.

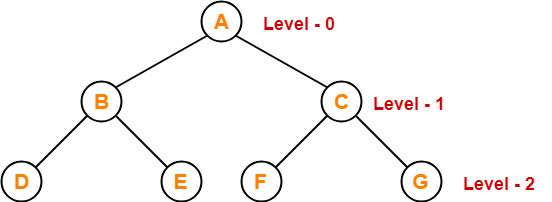
• Level-
• In a tree, each step from top to bottom is called the level of a tree.
• The level count starts with 0 and increments by 1 at each level or step.
• Example-

• Height-
• The total number of edges that lies on the longest path from any leaf node to a particular node is called as height of that node.
• The height of a tree is the height of the root node.
• Height of all leaf nodes = 0
• Example-

• Here,
• Height of node A = 3
• Height of node B = 2
• Height of node C = 2
• Height of node D = 0
• Height of node E = 1
• Height of node F = 0
• Height of node G = 1
• Height of node H = 0
• Height of node I = 0
• Height of node J = 0
• Height of node K = 0
• Depth-
• The total number of edges from root node to a particular node is called as depth of that node.
• The depth of a tree is the total number of edges from root node to a leaf node in the longest path.
• Depth of the root node = 0
• The terms “level” and “depth” are used interchangeably.
• Example-

• Here,
• Depth of node A = 0
• Depth of node B = 1
• Depth of node C = 1
• Depth of node D = 2
• Depth of node E = 2
• Depth of node F = 2
• Depth of node G = 2
• Depth of node H = 2
• Depth of node I = 3
• Depth of node J = 3
• Depth of node K = 3
• Subtree-
• In a tree, each child from a node forms a subtree recursively.
• Every child node forms a subtree on its parent node.
• Example-

• Forest-
• A forest is a set of disjoint trees.
• Example-

Binary Tree-

• Binary tree is a special tree data structure in which each node can have at most 2 children.
• Thus, in a binary tree,
• Each node has either 0 child or 1 child or 2 children.
• Example-

• Unlabeled Binary Tree-
• A binary tree is unlabeled if its nodes are not assigned any label.

• Example-
• Consider we want to draw all the binary trees possible with 3 unlabeled nodes.
• Using the above formula, we have-
• Number of binary trees possible with 3 unlabeled nodes

• Thus,
• With 3 unlabeled nodes, 5 unlabeled binary trees are possible.
• These unlabeled binary trees are as follows-

• Labeled Binary Tree-
• A binary tree is labeled if all its nodes are assigned a label.

• Example-
• Consider we want to draw all the binary trees possible with 3 labeled nodes.
• Using the above formula, we have-
• Number of binary trees possible with 3 labeled nodes

• Thus,
• With 3 labeled nodes, 30 labeled binary trees are possible.
• Each unlabeled structure gives rise to 3! = 6 different labeled structures.

• Similarly,
• Every other unlabeled structure gives rise to 6 different labeled structures.
• Thus, in total 30 different labeled binary trees are possible.

Types of Binary Trees-

• Rooted Binary Tree- A rooted binary tree is a binary tree that satisfies the following 2 properties-
• It has a root node.
• Each node has at most 2 children.
• Example-

• Full / Strictly Binary Tree- A binary tree in which every node has either 0 or 2 children is called a Full binary tree.
• Full binary tree is also called a Strictly binary tree.
• Example-

• Here,
• The first binary tree is not a full binary tree.
• This is because node C has only 1 child.
• Complete / Perfect Binary Tree - A complete binary tree is a binary tree that satisfies the following 2 properties-
• Every internal node has exactly 2 children.
• All the leaf nodes are at the same level.
• A complete binary tree is also called a Perfect binary tree.
• Example-

• Here,
• A first binary tree is not a complete binary tree.
• This is because all the leaf nodes are not at the same level.
• Almost Complete Binary Tree- An almost complete binary tree is a binary tree that satisfies the following 2 properties-
• All the levels are completely filled except possibly the last level.
• The last level must be strictly filled from left to right.
• Example-

• Here,
• A first binary tree is not an almost complete binary tree.
• This is because the last level is not filled from left to right.
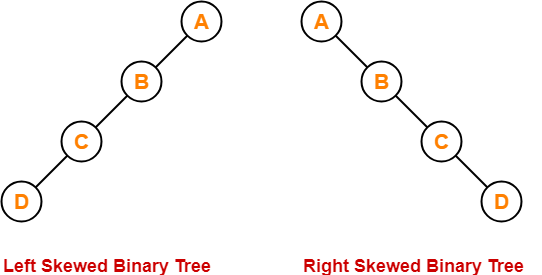
• Skewed Binary Tree - A skewed binary tree is a binary tree that satisfies the following 2 properties-
• All the nodes except one node have one and only one child.
• The remaining node has no child. 'OR'
• A skewed binary tree is a binary tree of n nodes such that its depth is (n-1).
• Example-

Binary Tree Properties-

• Minimum number of nodes in a binary tree of height H = H + 1
• Example - To construct a binary tree of height = 4, we need at least 4 + 1 = 5 nodes.

• Maximum number of nodes in a binary tree of height H = 2^(H+1) – 1
• Example - Maximum number of nodes in a binary tree of height 3

• Thus, in a binary tree of height = 3, a maximum number of nodes that can be inserted = 15.

• We can not insert more number of nodes in this binary tree.
• Total Number of leaf nodes in a Binary Tree = Total Number of nodes with 2 children + 1
• Example - Consider the following binary tree-

• Here,
• Number of leaf nodes = 3
• Number of nodes with 2 children = 2
• Clearly, the number of leaf nodes is one greater than the number of nodes with 2 children.
• This verifies the above relation.
• NOTE It is interesting to note that-Number of leaf nodes in any binary tree depends only on the number of nodes with 2 children.
• Maximum number of nodes at any level ‘L’ in a binary tree
  
• Example - Maximum number of nodes at level-2 in a binary tree

• Thus, in a binary tree, the maximum number of nodes that can be present at level-2 = 4.

Tree Traversal-

• Tree Traversal refers to the process of visiting each node in a tree data structure exactly once.

Depth First Traversal-

• Following three traversal techniques fall under Depth First Traversal-
1. Preorder Traversal
2. Inorder Traversal
3. Postorder Traversal
• Preorder Traversal-
• Algorithm-
1. Visit the root
2. Traverse the left subtree i.e. call Preorder (left subtree)
3. Traverse the right subtree i.e. call Preorder (right subtree)

Root → Left → Right

• Example-

• Preorder Traversal Shortcut - Traverse the entire tree starting from the root node keeping yourself to the left.

• Applications-
• Preorder traversal is used to get prefix expression of an expression tree.
• Preorder traversal is used to create a copy of the tree.
• Inorder Traversal-
• Algorithm-
1. Traverse the left subtree i.e. call Inorder (left subtree)
2. Visit the root
3. Traverse the right subtree i.e. call Inorder (right subtree)

Left → Root → Right

• Example-

• Inorder Traversal Shortcut - Keep a plane mirror horizontally at the bottom of the tree and take the projection of all the nodes.

• Application-
• Inorder traversal is used to get the infix expression of an expression tree.
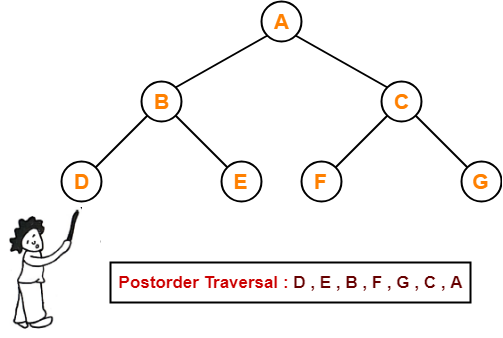
• Postorder Traversal-
• Algorithm-
1. Traverse the left subtree i.e. call Postorder (left subtree)
2. Traverse the right subtree i.e. call Postorder (right subtree)
3. Visit the root

Left → Right → Root

• Example-

• Postorder Traversal Shortcut - Pluck all the leftmost leaf nodes one by one.

• Applications-
• Postorder traversal is used to get the postfix expression of an expression tree.
• Postorder traversal is used to delete the tree.
• This is because it deletes the children first and then it deletes the parent.

Breadth-First Traversal-

• Breadth-First Traversal of a tree prints all the nodes of a tree level by level.
• Breadth-First Traversal is also called Level Order Traversal.
• Example-

• Application-
• Level order traversal is used to print the data in the same order as stored in the array representation of a complete binary tree.

Binary Search Tree-

• A binary Search Tree is a special kind of binary tree in which nodes are arranged in a specific order.
• In a binary search tree (BST), each node contains-
• Only smaller values in its left subtree
• Only larger values in its right subtree
• Example-

• Number of Binary Search Trees-

• Example - Number of distinct binary search trees possible with 3 distinct keys

• If three distinct keys are A, B, and C, then 5 distinct binary search trees are-

Binary Search Tree Construction-

• Let us understand the construction of a binary search tree using the following example-
• Example-
• Construct a Binary Search Tree (BST) for the following sequence of numbers-

50, 70, 60, 20, 90, 10, 40, 100

• When elements are given in a sequence,
• Always consider the first element as the root node.
• Consider the given elements and insert them in the BST one by one.
• The binary search tree will be constructed as explained below-
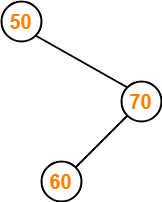
• Insert 50-

• Insert 70 - As 70 > 50, so insert 70 to the right of 50.

• Insert 60-
• As 60 > 50, so insert 60 to the right of 50.
• As 60 < 70, so insert 60 to the left of 70.

• Insert 20-
• As 20 < 50, so insert 20 to the left of 50.

• Insert 90-
• As 90 > 50, so insert 90 to the right of 50.
• As 90 > 70, so insert 90 to the right of 70.

• Insert 10-
• As 10 < 50, so insert 10 to the left of 50.
• As 10 < 20, so insert 10 to the left of 20.

• Insert 40-
• As 40 < 50, so insert 40 to the left of 50.
• As 40 > 20, so insert 40 to the right of 20.

• Insert 100-
• As 100 > 50, so insert 100 to the right of 50.
• As 100 > 70, so insert 100 to the right of 70.
• As 100 > 90, so insert 100 to the right of 90.

BST Traversal-

• A binary search tree is traversed in exactly the same way a binary tree is traversed.
• In other words, BST traversal is the same as binary tree traversal.
• Example-

• Now, let us write the traversal sequences for this binary search tree-
• Preorder Traversal-

100 , 20 , 10 , 30 , 200 , 150 , 300

• Inorder Traversal-

10 , 20 , 30 , 100 , 150 , 200 , 300

• Postorder Traversal-

10 , 30 , 20 , 150 , 300 , 200 , 100

• Important Notes-
• Note-01: 
• Inorder traversal of a binary search tree always yields all the nodes in increasing order.
• Note-02:
• A binary search tree can be constructed using only preorder or only postorder traversal results.
• This is because inorder traversal can be obtained by sorting the given result in increasing order.

Binary Search Tree Operations-

Search Operation-

• Search Operation is performed to search a particular element in the Binary Search Tree.
• Rules - For searching a given key in the BST,
• Compare the key with the value of the root node.
• If the key is present at the root node, then return the root node.
• If the key is greater than the root node value, then recur for the root node’s right subtree.
• If the key is smaller than the root node value, then recur for the root node’s left subtree.
• Example - Consider key = 45 has to be searched in the given BST-

• We start our search from the root node 25.
• As 45 > 25, so we search in 25’s right subtree.
• As 45 < 50, so we search in 50’s left subtree.
• As 45 > 35, so we search in 35’s right subtree.
• As 45 > 44, so we search in 44’s right subtree but 44 has no subtrees.
• So, we conclude that 45 is not present in the above BST.

Insertion Operation-

• Insertion Operation is performed to insert an element in the Binary Search Tree.
• Rules-
• The insertion of a new key always takes place as the child of some leaf node.
• For finding out the suitable leaf node,
• Search the key to be inserted from the root node till some leaf node is reached.
• Once a leaf node is reached, insert the key as child of that leaf node.
• Example - Consider the following example where key = 40 is inserted in the given BST-

• We start searching for value 40 from the root node 100.
• As 40 < 100, we search in 100’s left subtree.
• As 40 > 20, so we search in 20’s right subtree.
• As 40 > 30, we add 40 to 30’s right subtree.

Deletion Operation-

• Deletion Operation is performed to delete a particular element from the Binary Search Tree.
• When it comes to deleting a node from the binary search tree, the following three cases are possible-
• Case-01: Deletion Of A Node Having No Child (Leaf Node)-
• Just remove/disconnect the leaf node that is to delete from the tree.
• Example - Consider the following example where the node with value = 20 is deleted from the BST-

• Case-02: Deletion Of A Node Having Only One Child-
• Just make the child of the deleting node, the child of its grandparent.
• Example - Consider the following example where node with value = 30 is deleted from the BST-

• Case-02: Deletion Of A Node Having Two Children-
• A node with two children may be deleted from the BST in the following two ways-
• Method-01:
• Visit the right subtree of the deleting node.
• Pluck the least value element called as inorder successor.
• Replace the deleting element with its inorder successor.
• Example - Consider the following example where node with value = 15 is deleted from the BST-

• Method-02:
• Visit the left subtree of the deleting node.
• Pluck the greatest value element called the inorder predecessor.
• Replace the deleting element with its inorder predecessor.
• Example - Consider the following example where node with value = 15 is deleted from the BST-

Time Complexity-

• The time complexity of all BST Operations = O(h).
• Here, h = Height of binary search tree

Now, let us discuss the worst case and best case.

• Worst Case-
• The binary search tree is a skewed binary search tree.
• The height of the binary search tree becomes n.
• So, the Time complexity of BST Operations = O(n).
• In this case, a binary search tree is as good as an unordered list with no benefits.

• Best Case-
• The binary search tree is a balanced binary search tree.
• The height of the binary search tree becomes log(n).
• So, the Time complexity of BST Operations = O(logn).

AVL Tree-

• AVL trees are a special kind of binary search tree.
• In AVL trees, the height of the left subtree and right subtree of every node differs by at most one.
• AVL trees are also called self-balancing binary search trees.
• Example - Following tree is an example of AVL tree-

• This tree is an AVL tree because-
• It is a binary search tree.
• The difference between the height of the left subtree and right subtree of every node is at most one.
• Following tree is not an example of AVL Tree-

• This tree is not an AVL tree because-
• The difference between the height of the left subtree and the right subtree of the root node = 4 – 2 = 2.
• This difference is greater than one.

Balance Factor-

• Balance factor is defined for every node.
• Balance factor of a node = height of its left subtree – height of its right subtree
• In AVL tree, the Balance factor of every node is either 0 or 1 or -1.

AVL Tree Properties-

• Property-01: Maximum possible number of nodes in AVL tree of height H
• Example - Maximum possible number of nodes in AVL tree of height-3

• Thus, in the AVL tree of height-3, the maximum number of nodes that can be inserted = 15.

• We can not insert more number of nodes in this AVL tree.
• Property-02:
• The minimum number of nodes in AVL Tree of height H is given by a recursive relation- N(H) = N(H-1) + N(H-2) + 1
• Base conditions for this recursive relation are-
• N(0) = 1
• N(1) = 2
• Example - Minimum possible number of nodes in AVL tree of height-3 = 7

• Property-03: Minimum possible height of AVL Tree using N nodes
• Example - Minimum possible height of AVL Tree using 8 nodes

• Property-04: Maximum height of AVL Tree using N nodes is calculated using recursive relation- N(H) = N(H-1) + N(H-2) + 1
• Base conditions for this recursive relation are-
• N(0) = 1
• N(1) = 2

AVL Tree Operations-

• Search Operation
• Insertion Operation
• Deletion Operation

Insertion in AVL Tree-

• Insertion Operation is performed to insert an element in the AVL Tree.
• To insert an element in the AVL tree, follow the following steps-
• Insert the element in the AVL tree in the same way the insertion is performed in BST.
• After insertion, check the balance factor of each node of the resulting tree.
• Now, following two cases are possible-
• Case-01:
• After the insertion, the balance factor of each node is either 0 or 1 or -1.
• In this case, the tree is considered to be balanced.
• Conclude the operation.
• Insert the next element if any.
• Case-02:
• After the insertion, the balance factor of at least one node is not 0 or 1 or -1.
• In this case, the tree is considered to be imbalanced.
• Perform the suitable rotation to balance the tree.
• After the tree is balanced, insert the next element if any.
• PRACTICE PROBLEM BASED ON AVL TREE INSERTION-
• Construct AVL Tree for the following sequence of numbers-

50 , 20 , 60 , 10 , 8 , 15 , 32 , 46 , 11 , 48

• Solution-
• Step-01: Insert 50

• Step-02: Insert 20 - As 20 < 50, so insert 20 in 50’s left sub tree.

• Step-03: Insert 60 - As 60 > 50, so insert 60 in 50’s right sub tree.

• Step-04: Insert 10
• As 10 < 50, so insert 10 in 50’s left subtree.
• As 10 < 20, so insert 10 in 20’s left sub tree.

• Step-05: Insert 8
• As 8 < 50, so insert 8 in 50’s left subtree.
• As 8 < 20, so insert 8 in 20’s left subtree.
• As 8 < 10, so insert 8 in 10’s left subtree.

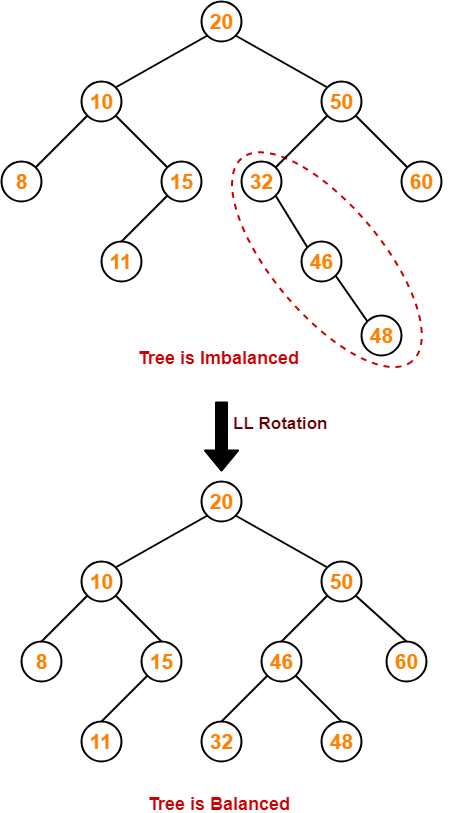
• To balance the tree,
• Find the first imbalanced node on the path from the newly inserted node (node 8) to the root node.
• The first imbalanced node is node 20.
• Now, count three nodes from node 20 in the direction of the leaf node.
• Then, use AVL tree rotation to balance the tree.

• Step-06: Insert 15
• As 15 < 50, so insert 15 in 50’s left subtree.
• As 15 > 10, so insert 15 in 10’s right subtree.
• As 15 < 20, so insert 15 in 20’s left subtree.

• To balance the tree,
• Find the first imbalanced node on the path from the newly inserted node (node 15) to the root node.
• The first imbalanced node is node 50.
• Now, count three nodes from node 50 in the direction of the leaf node.
• Then, use AVL tree rotation to balance the tree.

• Step-07: Insert 32
• As 32 > 20, so insert 32 in 20’s right subtree.
• As 32 < 50, so insert 32 in 50’s left subtree.

• Step-08: Insert 46
• As 46 > 20, so insert 46 in 20’s right subtree.
• As 46 < 50, so insert 46 in 50’s left subtree.
• As 46 > 32, so insert 46 in 32’s right subtree.

• Step-09: Insert 11
• As 11 < 20, so insert 11 in 20’s left subtree.
• As 11 > 10, so insert 11 in 10’s right subtree.
• As 11 < 15, so insert 11 in 15’s left subtree.

• Step-10: Insert 48
• As 48 > 20, so insert 48 in 20’s right subtree.
• As 48 < 50, so insert 48 in 50’s left subtree.
• As 48 > 32, so insert 48 in 32’s right subtree.
• As 48 > 46, so insert 48 in 46’s right subtree.

• To balance the tree,
• Find the first imbalanced node on the path from the newly inserted node (node 48) to the root node.
• The first imbalanced node is node 32.
• Now, count three nodes from node 32 in the direction of the leaf node.
• Then, use AVL tree rotation to balance the tree.

AVL Tree Rotations-

• Rotation is the process of moving the nodes to make tree balanced.
• Kinds of Rotations - There are 4 kinds of rotations possible in AVL Trees-

• Cases Of Imbalance And Their Balancing Using Rotation Operations-
• Case-01:

• Case-02:

• Case-03:

• Case-04:

Heap Data Structure-

• In data structures,
• Heap is a specialized data structure.
• It has special characteristics.
• A heap may be implemented using an n-ary tree.

Binary Heap - A binary heap is a Binary Tree with the following two properties-

• Ordering Property - By this property,
• Elements in the heap tree are arranged in a specific order.
• This gives rise to two types of heaps- min heap and max heap.
• Structural Property - By this property,
• A binary heap is an almost complete binary tree.
• It has all its levels completely filled except possibly the last level.
• The last level is strictly filled from left to right.
• Types of Binary Heap - Depending on the arrangement of elements, a binary heap may be of the following two types-

• Max Heap-
• Max Heap conforms to the above properties of the heap.
• In a max heap, every node contains a greater or equal value element than its child nodes.
• Thus, the root node contains the largest value element.
• Example-

• This is maxed heap because-
• Every node contains a greater or equal value element than its child nodes.
• It is an almost complete binary tree with its last level strictly filled from left to right.
• Min Heap-
• Min Heap conforms to the above properties of the heap.
• In min-heap, every node contains a lesser value element than its child nodes.
• Thus, the root node contains the smallest value element.
• Example-

• This is min-heap because-
• Every node contains a lesser value element than its child nodes.
• It is an almost complete binary tree with its last level strictly filled from left to right.

Array Representation of Binary Heap-

• A binary heap is typically represented as an array.

• For a node present at index ‘i’ of the array Arr-
• If indexing starts with 0,
• Its parent node will be present at array location = Arr [ i/2 ]
• Its left child node will be present at array location = Arr [ 2i+1 ]
• Its right child node will be present at array location = Arr [ 2i+2 ]
• If indexing starts with 1,
• Its parent node will be present at array location = Arr [ ⌊i/2⌋ ]
• Its left child node will be present at array location = Arr [ 2i ]
• Its right child node will be present at array location = Arr [ 2i+1 ]

Important Notes-

• Note-01:
• Level order traversal technique may be used to achieve the array representation of a heap tree.
• Array representation of a heap never contains any empty indices in between.
• However, the array representation of a binary tree may contain some empty indices in between.
• Note-02: Given an array representation of a binary heap,
• If all the elements are in descending order, then heap is definitely a max heap.
• If all the elements are not in descending order, then it may or may not be a max heap.
• If all the elements are in ascending order, then the heap is definitely a min-heap.
• If all the elements are not in ascending order, then it may or may not be a min-heap.
• Note-03:
• In a max heap, every node contains a greater or equal value element than all its descendants.
• In min-heap, every node contains a smaller value element than all its descendants.

Heap Operations-

• Here, we will discuss how these operations are performed on a max heap.
• Max Heap Operations - We will discuss the construction of a max heap and how the following operations are performed on a max heap-
• Finding Maximum Operation
• Insertion Operation
• Deletion Operation
• Max Heap Construction - Given an array of elements, the steps involved in constructing a max heap are-
• Step-01:
• Convert the given array of elements into an almost complete binary tree.
• Step-02: Ensure that the tree is a max heap.
• Check that every non-leaf node contains a greater or equal value element than its child nodes.
• If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
• Start checking from a non-leaf node with the highest index (bottom to top and right to left).

Finding Maximum Operation-

• In max heap, the root node always contains the maximum value element.
• So, we directly display the root node value as the maximum value in max heap.

Insertion Operation-

• Insertion Operation is performed to insert an element in the heap tree.
• Step-01:
• Insert the new element as a next leaf node from left to right.
• Step-02: Ensure that the tree remains a max heap.
• Check that every non-leaf node contains a greater or equal value element than its child nodes.
• If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
• Start checking from a non-leaf node with the highest index (bottom to top and right to left).

Deletion Operation-

• Deletion Operation is performed to delete a particular element from the heap tree.
• When it comes to deleting a node from the heap tree, following two cases are possible-
• Case-01: Deletion Of Last Node-
• This case is pretty simple.
• Just remove / disconnect the last leaf node from the heap tree.
• Case-02: Deletion Of Some Other Node-
• This case is little bit difficult.
• Deleting a node other than the last node disturbs the heap properties.
• The steps involved in deleting such a node are-
• Step-01:
• Delete the desired element from the heap tree.
• Pluck the last node and put it in place of the deleted node.
• Step-02: Ensure that the tree remains a max heap.
• Check that every non-leaf node contains a greater or equal value element than its child nodes.
• If there exists any node that does not satisfies the ordering property of max heap, swap the elements.
• Start checking from a non-leaf node with the highest index (bottom to top and right to left).

B-tree

• B-tree is a special type of self-balancing search tree in which each node can contain more than one key and can have more than two children. It is a generalized form of the binary search tree.
• It is also known as a height-balanced m-way tree.

B-tree Properties

1. For each node x, the keys are stored in increasing order.
2. In each node, there is a boolean value x.leaf which is true if x is a leaf.
3. If n is the order of the tree, each internal node can contain at most n - 1 keys along with a pointer to each child.
4. Each node except root can have at most n children and at least n/2 children.
5. All leaves have the same depth (i.e. height-h of the tree).
6. The root has at least 2 children and contains a minimum of 1 key.
7. If n ≥ 1, then for any n-key B-tree of height h and minimum degree t ≥ 2, h ≥ logt (n+1)/2.

Operations on a B-tree

• Searching an element in a B-tree - Searching for an element in a B-tree is the generalized form of searching an element in a Binary Search Tree. The following steps are followed.
1. Starting from the root node, compare k with the first key of the node.
2. If k = the first key of the node, return the node and the index.
3. If k.leaf = true, return NULL (i.e. not found).
4. If k < the first key of the root node, search the left child of this key recursively.
• If there is more than one key in the current node and k > the first key, compare k with the next key in the node.
• If k < next key, search the left child of this key (ie. k lies in between the first and the second keys).
• Else, search the right child of the key.
5. Repeat steps 1 to 4 until the leaf is reached.
• Searching Example
• Let us search key k = 17 in the tree below degree 3.

• k is not found in the root so, compare it with the root key.

• Since k > 11, go to the right child of the root node

• Compare k with 16. Since k > 16, compare k with the next key 18

• Since k < 18, k lies between 16 and 18. Search in the right child of 16 or the left child of 18.

• k is found.

Insertion Operation

1. If the tree is empty, allocate a root node and insert the key.
2. Update the allowed number of keys in the node.
3. Search the appropriate node for insertion.
4. If the node is full, follow the steps below.
5. Insert the elements in increasing order.
6. Now, there are elements greater than its limit. So, split at the median.
7. Push the median key upwards and make the left keys as a left child and the right keys as a right child.
8. If the node is not full, follow the steps below.
9. Insert the node in increasing order.

• Insertion Example
• The elements to be inserted are 8, 9, 10, 11, 15, 20, 17.

• Deletion Operation - Before going through the steps below, one must know these facts about a B tree of degree m.
1. A node can have a maximum of m children. (i.e. 3)
2. A node can contain a maximum of m - 1 keys. (i.e. 2)
3. A node should have a minimum of ⌈m/2⌉ children. (i.e. 2)
4. A node (except root node) should contain a minimum of ⌈m/2⌉ - 1 keys. (i.e. 1)
• There are three main cases for deletion operation in a B tree.
• Case I
• The key to being deleted lies in the leaf. There are two cases for it.
• The deletion of the key does not violate the property of the minimum number of keys a node should hold.
• In the tree below, deleting 32 does not violate the above properties.

• The deletion of the key violates the property of the minimum number of keys a node should hold. In this case, we borrow a key from its immediate neighboring sibling node in the order of left to right.
• First, visit the immediate left sibling. If the left sibling node has more than a minimum number of keys, then borrow a key from this node.
• Else, check to borrow from the immediate right sibling node.
• In the tree below, deleting 31 results in the above condition. Let us borrow a key from the left sibling node.

• If both the immediate sibling nodes already have a minimum number of keys, then merge the node with either the left sibling node or the right sibling node. This merging is done through the parent node.
• Deleting 30 results in the above case.

• Case II
• If the key to be deleted lies in the internal node, the following cases occur.
• The internal node, which is deleted, is replaced by an inorder predecessor if the left child has more than the minimum number of keys.

• The internal node, which is deleted, is replaced by an inorder successor if the right child has more than the minimum number of keys.
• If either child has exactly a minimum number of keys then, merge the left and the right children.

• After merging if the parent node has less than the minimum number of keys then, look for the siblings as in Case I.
• Case III
• In this case, the height of the tree shrinks. If the target key lies in an internal node, and the deletion of the key leads to a fewer number of keys in the node (i.e. less than the minimum required), then look for the inorder predecessor and the inorder successor. If both the children contain a minimum number of keys then, borrowing cannot take place. This leads to Case II(3) i.e. merging the children.
• Again, look for the sibling to borrow a key. But, if the sibling also has only a minimum number of keys then, merge the node with the sibling along with the parent. Arrange the children accordingly (increasing order).

Red-Black Tree

• A red-Black tree is a self-balancing binary search tree in which each node contains an extra bit for denoting the color of the node, either red or black.
• A red-black tree satisfies the following properties:

1. Red/Black Property: Every node is colored, either red or black.
2. Root Property: The root is black.
3. Leaf Property: Every leaf (NIL) is black.
4. Red Property: If a red node has children then, the children are always black.
5. Depth Property: For each node, any simple path from this node to any of its descendant leaf has the same black depth (the number of black nodes).

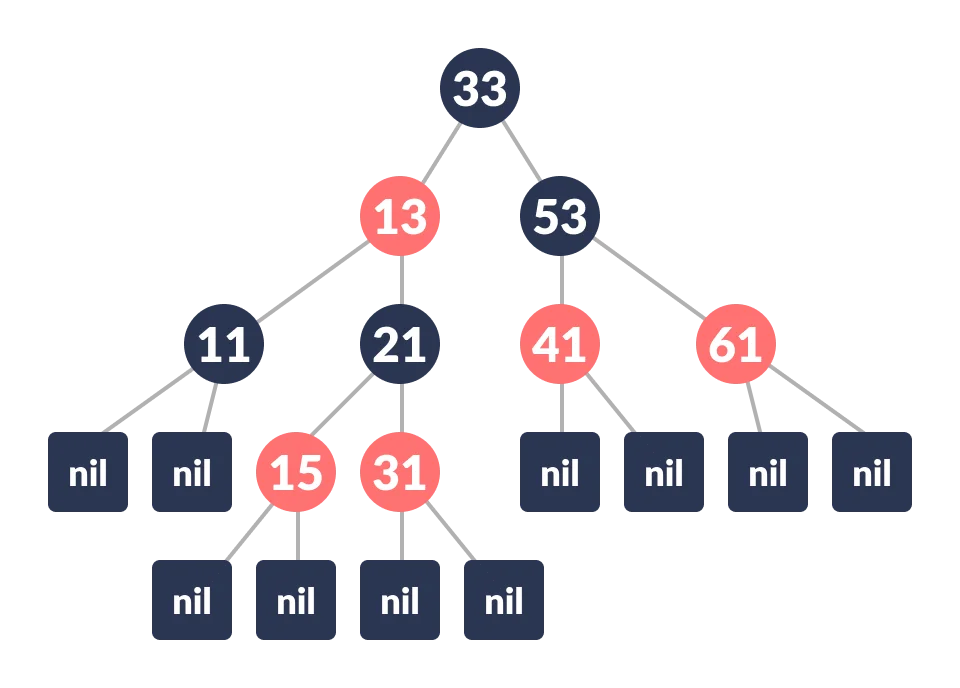
• An example of a red-black tree is:

• Each node has the following attributes:
• color
• key
• leftChild
• rightChild
• parent (except root node)
• How the red-black tree maintains the property of self-balancing?
• The red-black color is meant for balancing the tree.
• The limitations put on the node colors ensure that any simple path from the root to a leaf is not more than twice as long as any other such path. It helps in maintaining the self-balancing property of the red-black tree.

Operations on a Red-Black Tree

• Various operations that can be performed on a red-black tree are:
• Rotating the subtrees in a Red-Black Tree
• In rotation operation, the positions of the nodes of a subtree are interchanged.
• Rotation operation is used for maintaining the properties of a red-black tree when they are violated by other operations such as insertion and deletion.
• There are two types of rotations:
• Left Rotate
• In the left rotation, the arrangement of the nodes on the right is transformed into the arrangements on the left node.
• Algorithm
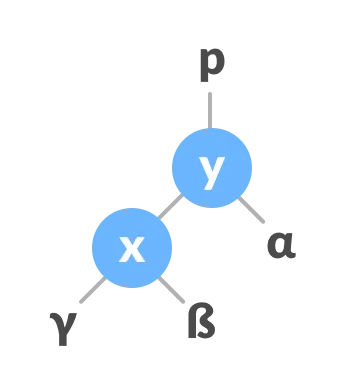
• Let the initial tree be

• If y has a left subtree, assign x as the parent of the left subtree of y

• If the parent of x is NULL, make y the root of the tree.
• Else if x is the left child of p, make y as the left child of p.
• Else assign y as the right child of p.

• Make y as the parent of x.

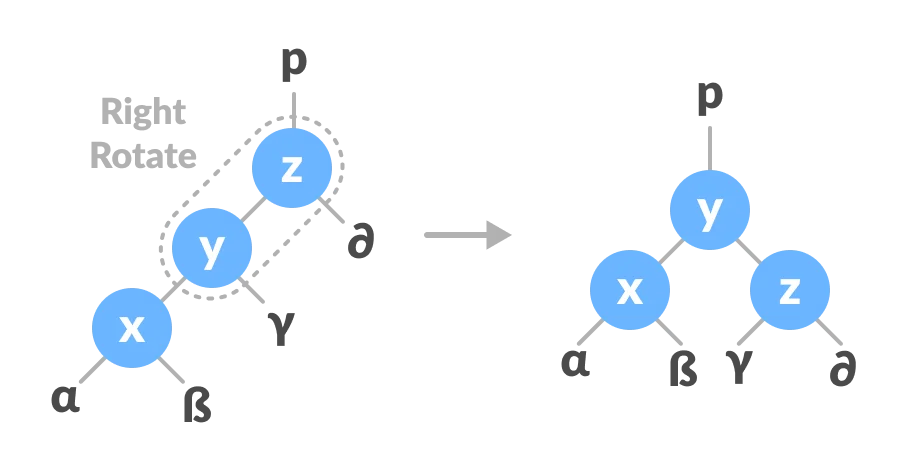
• Right Rotate
• In right rotation, the arrangement of the nodes on the left is transformed into the arrangements on the right node.
• Let the initial tree be:

• If x has a right subtree, assign y as the parent of the right subtree of x

• If the parent of y is NULL, make x as the root of the tree.
• Else if y is the right child of its parent p, make x as the right child of p.
• Else assign x as the left child of p

• Make x as the parent of y.

• Left-Right and Right-Left Rotate
• In left-right rotation, the arrangements are first shifted to the left and then to the right.
• Do left rotation on x-y.

• Do right rotation on y-z

• In right-left rotation, the arrangements are first shifted to the right and then to the left.
• Do right rotation on x-y

• Do left rotation on z-y.

Inserting an element into a Red-Black Tree

• While inserting a new node, the new node is always inserted as a RED node. After insertion of a new node, if the tree is violating the properties of the red-black tree then, we do the following operations.
• Recolor
• Rotation

Algorithm to insert a node

1. Let y be the leaf (ie. NIL) and x be the root of the tree.
2. Check if the tree is empty (ie. whether x is NIL). If yes, insert newNode as a root node and color it black.
3. Else, repeat steps following steps until leaf (NIL) is reached.
1. Compare newKey with rootKey.
2. If newKey is greater than rootKey, traverse through the right subtree.
3. Else traverse through the left subtree.
4. Assign the parent of the leaf as a parent of newNode.
5. If leafKey is greater than newKey, make newNode as rightChild.
6. Else, make newNode as leftChild.
7. Assign NULL to the left and rightChild of newNode.
8. Assign RED color to newNode.
9. Call InsertFix-algorithm to maintain the property of red-black tree if violated.

• Why newly inserted nodes are always red in a red-black tree?
• This is because inserting a red node does not violate the depth property of a red-black tree.
• If you attach a red node to a red node, then the rule is violated but it is easier to fix this problem than the problem introduced by violating the depth property.
• Algorithm to maintain the red-black property after insertion
• This algorithm is used for maintaining the property of a red-black tree if the insertion of a newNode violates this property.
1. Do the following while the parent of newNode p is RED.
2. If p is the left child of grandParent gP of z, do the following.
• Case-I:
• If the color of the right child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
• Assign gP to newNode.
• Case-II:
• Else if newNode is the right child of p then, assign p to newNode.
• Left-Rotate newNode.
• Case-III:
• Set color of p as BLACK and color of gP as RED.
• Right-Rotate gP.
3. Else, do the following.
• If the color of the left child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
• Assign gP to newNode.
• Else if newNode is the left child of p then, assign p to newNode and Right-Rotate newNode.
• Set color of p as BLACK and color of gP as RED.
• Left-Rotate gP.
4. Set the root of the tree as BLACK.

Deleting an element from a Red-Black Tree

• This operation removes a node from the tree. After deleting a node, the red-black property is maintained again.
• Algorithm to delete a node

1. Save the color of nodeToBeDeleted in origrinalColor.
2. f the left child of nodeToBeDeleted is NULL
1. Assign the right child of nodeToBeDeleted to x.
2. Transplant nodeToBeDeleted with x.
3. Else if the right child of nodeToBeDeleted is NULL
1. Assign the left child of nodeToBeDeleted into x.
2. Transplant nodeToBeDeleted with x.
4. Else
1. Assign the minimum of right subtree of noteToBeDeleted into y.
2. Save the color of y in originalColor.
3. Assign the rightChild of y into x.
4. If y is a child of nodeToBeDeleted, then set the parent of x as y.
5. Else, transplant y with rightChild of y.
6. Transplant nodeToBeDeleted with y.
7. Set the color of y with originalColor.
5. If the originalColor is BLACK, call DeleteFix(x).

Algorithm to maintain Red-Black property after deletion

• This algorithm is implemented when a black node is deleted because it violates the black depth property of the red-black tree.
• This violation is corrected by assuming that node x (which is occupying y's original position) has an extra black. This makes node x neither red nor black. It is either doubly black or black-and-red. This violates the red-black properties.
• However, the color attribute of x is not changed rather the extra black is represented in x's pointing to the node.
• The extra black can be removed if

1. It reaches the root node.
2. If x points to a red-black node. In this case, x is colored black.
3. Suitable rotations and recoloring are performed.

• The following algorithm retains the properties of a red-black tree.

1. Do the following until the x is not the root of the tree and the color of x is BLACK
2. If x is the left child of its parent then,
• Assign w to the sibling of x.
• If the right child of parent of x is RED,
• Case-I:
1. Set the color of the right child of the parent of x as BLACK.
2. Set the color of the parent of x as RED.
3. Left-Rotate the parent of x.
4. Assign the rightChild of the parent of x to w.
• If the color of both the right and the leftChild of w is BLACK,
• Case-II:
1. Set the color of w as RED
2. Assign the parent of x to x.
• Else if the color of the rightChild of w is BLACK
• Case-III:
1. Set the color of the leftChild of w as BLACK
2. Set the color of w as RED
3. Right-Rotate w.
4. Assign the rightChild of the parent of x to w.
• If any of the above cases do not occur, then do the following.
• Case-IV:
1. Set the color of w as the color of the parent of x.
2. Set the color of the parent of x as BLACK.
3. Set the color of the right child of w as BLACK.
4. Left-Rotate the parent of x.
5. Set x as the root of the tree.
3. Else the same as above with right changed to left and vice versa.
4. Set the color of x as BLACK.